十进制二进制转换(二进制转十进制最简单的算法)
上周末,给孩子辅导奥数的时候,发现居然有一道二进制题,题目是求两个二进制的和。我的视频课第一课中就介绍了二进制的特点“逢二进一,借一当二”,给孩子讲了下,他还是顺利的做了出来。然后,我又给孩子讲了下十进制与二进制的转换。在讲十进制与二进制转换的时候,我是按照咱们以前学的除二取余法,如下图所示:
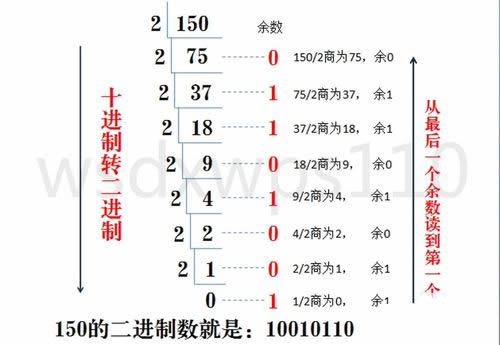
这种算法应该说是教科书的算法,去各大搜索引擎搜出来的算法都是这个。
我大概比别人多思考了一步,我在想为什么要除2取余,经过思考我发现其实质是要找出这个数里面含有多少个2,例如例图中的150,它的里面就含有75个2,而2的二进制为10,也就是说要算出75个(10)₂的和。继续思考,你会发现,(10)₂ (10)₂=(100)₂=2² , (100)₂ (100)₂=(1000)₂=2³,于是我得出了如下图所示结果:
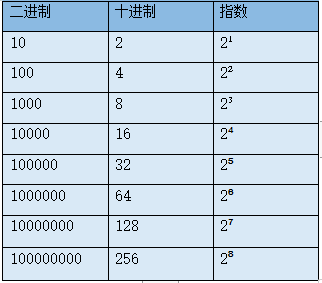
从上图中可以总结出一个规律:那就是2的指数是几,换算成二级制后面就有几个0,比如:2⁸=100000000。这个也好理解,我的视频课程讲ASCII码时,说ASCII码只占用了7位存储,最高位为0,所以最多可以存储128个字符,存储范围从00000000到01111111,也就是10进制的0-127。下图就是我的最新算法:

大家可以对比一下,看看是否简化了原先的除2取余算法。





